Gauge for Length of Day (showing Solstices & Equinoxes)

[guxdude]

it does triple the calls to $twcweather

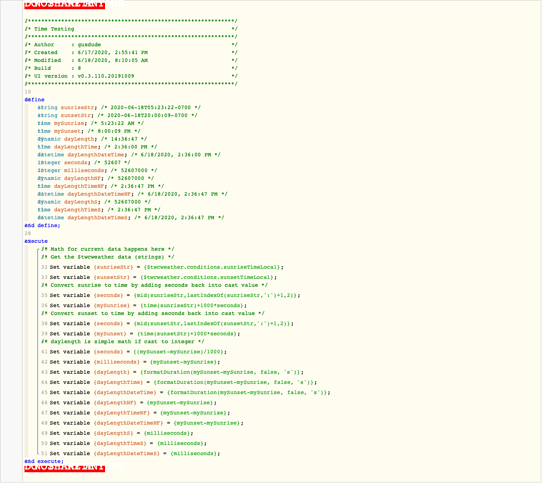
I thought these were just variables. I know they update periodically but assumed they were just static otherwise. Does each reference to $twcweather make some sort of call? I had a different implementation that stuck the values into intermediate variables and processed on that but I didn’t think it made a difference. That would do the same thing with just one ‘call’ for each value. I guess my other question is how do you convert to your sunrise/sunset variables from $twc given the time() conversion truncation?

[WCmore]

assumed they were just static

From what I can see, every $twcweather command pulls fresh data…
(even if the data has not updated in awhile)

---

how do you convert to your sunrise/sunset variables from $twc given the time() conversion truncation?

Two steps really. One piston runs daily and sticks the time into a global string:

---

… and then this piston takes that @global string, and does my previously mentioned math.

I mean, you could do both in the same piston… I just have mine set up to update at different times, with different parameters.

---

Pro Tip:

You probably want your @globals to only use a single @…
(not two like in my examples)

[guxdude]

@global string, and does my previously mentioned math

Sorry, I’m slow today. I think you showed here how you store the string {@@sunsetStr} and you showed above how you do calculations based on a time variable {@@sunset} but my problem was converting from a string to time as @@sunset=time(@@sunsetStr) would truncate the seconds. Was wondering if you had some trick other than what I did above to ensure you got the seconds.

[WCmore]

I don’t think I converted the string into Time… I just went thru the work to go the other way…
(converting the time into a string, LOL)

---

Highlights from my earlier posts:

I set the global:
time @sunrise 6:47:19 AM
time @sunset 7:12:47 PM

Then I subtract those @global times and store in a string {cur}. (first line below)

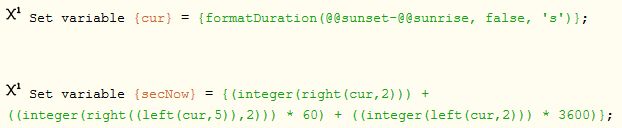
Then I parsed the string… (second) + (minute * 60) + (hour * 3600) (last line above)

This tells us the exact number of seconds that the sun is above the horizon…

[WCmore]

my problem was converting from a string to time as @@sunset=time(@@sunsetStr) would truncate the seconds

To answer this another way, here are the three steps I went with: (Time > String > Integer)

• I took the $twc sun times, and saved them as @global time
  IE: @sunrise = 6:47:19 AM and @sunset = 7:12:47 PM
• I subtracted the two @globals times, and stored answer in a local string {cur}
  IE: {cur} = 13:18:29
• I parsed that string using (second) + (minute * 60) + (hour * 3600),
  and stored the answer as an integer
  IE: {secNow} = 47909 <-- This is the number that is inputted into all of the other math

(it could really be done in 1 or 2 steps, but I want the @global for other pistons to use, and {cur} is a great abbreviation for my piston state)

---

Notice I manually do the math in the last step to assure that the seconds are counted.

Using my {cur} example above, this is: (29) + (18 * 60) + (13 * 3600)

(If you let webCoRE calculate normally, you will loose the precious seconds, due to flooring… which probably explains your 0.01% variance)

[fieldsjm]

As an alternative, I’ve been using a modified version of this piston to pull astronomical sunrise/set and conveniently they provide an day length integer in seconds.

Astronomical Data API

Having sunrise and sunset times for automation is great but… By default, both of these variables are limited to a resolution of whole minutes. I want that resolution down to the second. For my lighting, I want to be able to do some calculations for controlling the levels based on things like twilight, dusk, dawn, etc. I created this piston that calls an API which gives me the data and resolution I wanted. I have it setting global variables that I then use in various pistons. For exam…

As a backup, in case the API fails, I added the calculation using $twcweather data. Thanks for tip @WCmore to manually add each time component to ensure seconds are captured.

Now if I could only determine which is more accurate. When I compared the two data points, day length from the API is 30 seconds longer than the calculation using $twc data.

[WCmore]

Since APIs come and go… (and free today does not mean free tomorrow)…
I prefer using reliable internal data, whenever possible.
(I cannot fathom SmartThings ever dropping sunrise and sunset times)

---

When I compared the two data points, day length from the API is 30 seconds longer

30 second difference could simply be the data is pulled from 10 miles away.
(IE: a shorter day could mean the sensor is farther north)

… or it could be rounding to the whole minute…

[fieldsjm]

I prefer using reliable internal data, whenever possible.

I would generally agree. Too bad the internal data ($sunrise $sunset) doesn’t include seconds. And whose to say they (ST) won’t decide to switch up the weather service again.

30 second difference could simply be the data is pulled from 10 miles away.
(IE: a shorter day could mean the sensor is farther north)

… or it could be rounding to the whole minute…

Guessing it’s a location issue, each data point pulls seconds regardless of method (No :00 data points). Sunrise differs by 12 seconds and sunset by 18. Not aignificnat enough to stress over but an interesting observation.

[WCmore]

Guessing it’s a location issue … Sunrise differs by 12 seconds and sunset by 18

This gets me thinking…

IF both rise and set times are both shifted in the same direction…
(IE: both early, or both late)
then part of those values can represent a east/west shift.
(with the earlier location being farther east)

Using your example above, this could equate to 12 seconds east or west, and about 6 seconds north or south. (knights move in chess?)

I bet if you studied those variances for a few days, you’d be able to guesstimate where the reporting sensor(s) are located at. (just remember the variances are between the 2 stations… not your real location)

[WCmore]

For fun, I just ran a few numbers…

From the equator, on a typical day, in 12 seconds,
the sun can appear to travel about 3.5 miles to the west.

(based on Earths circumference / 24 = 1,038 mph)

This also means the farther away from the equator, the less miles per second from your perspective.
(IE: At latitude 60, that 12 seconds equates to about 1.75 miles)

[fieldsjm]

Interesting thought experiment. I wasn’t able to get into the full logic of the API but it appears to be calculating based on lat/long so theoretically more accurate to physical location?

Anyway, today, the sunrise API is 14 seconds earlier than the TWC data, north-west at approximately 2.2 miles is a weather station. Plugging in those coordinates into the API = almost identical data to the twc data (1 sec) .

[WCmore]

the sunrise API is 14 seconds earlier than the TWC data, north-west at approximately 2.2 miles is a weather station

If that is the right station, and we reverse engineer my previous formula, that estimates your GPS latitude somewhere between 36 and 44 degrees. (either north or south)

Note, I am not trying to blast your personal info here…
I’m just making a playful guess based on partial data.

I bet with a few days worth of data, we could estimate the latitude within one degree.
(however, longitude will never be revealed unless you also included the actual times…
… and even then, it would only tell you how far east/west in any given timezone)

---

the API … appears to be calculating based on lat/long so theoretically more accurate to physical location?

I thought SmartThings captured GPS coords when determining our Home location.
(Although I wonder at what level of precision that data is passed to $twcweather requests)

[fieldsjm]

If that is the right station, and we reverse engineer my previous formula, that estimates your GPS latitude somewhere between 36 and 44 degrees. (either north or south)

Note, I am not trying to blast your personal info here…
I’m just making a playful guess based on partial data.

I thought SmartThings captured GPS coords when determining our Home location.
(Although I wonder at what level of precision that data is passed to $twcweather requests)

ST does captured those coordinates. Based on our little experiment, if they are passed to $twcweather, they are only being used to determine the closest station.

[guxdude]

I manually do the math

Just to follow up on this from a few days ago. As I studied the numbers it appeared my DLP was still not changing daily. Digging in, I found that, even though I got all the times down to seconds, webcore still wouldn’t do all the right math with those times and was truncating. So I converted my shortest and longest day to seconds for the multiplier and then current day all using your formula and now I get (I think) a more accurate number. Today it says I am at 99.82% of max. Makes sense since max should be in a few days. Thanks!

[WCmore]

even though I got all the times down to seconds, webcore still wouldn’t do all the right math with those times and was truncating

This was probably the most frustrating part of this piston.
(and is why I now do all of my math based on integer seconds instead of Time)

[guxdude]

I’m sure you already knew this but I find it interesting that webcore can do the correct calculations
for a dynamic variable but not for a time or datetime variable. I put together a quick piston.

with these inputs:

and using the same formula:

I get these three results:

If we could just convert the dynamic variable directly to seconds it would be great. As soon as you do anything with time, seconds are truncated.

[WCmore]

I find it interesting that webcore can do the correct calculations
for a dynamic variable but not for a time or datetime variable

So which of the nine types is dynamic representing in this case?

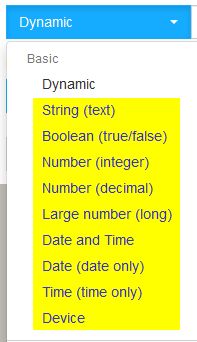
The only possibility I see is perhaps a string…
(since military time is not on the list)

[guxdude]

which of the nine types is dynamic representing

Regardless of what it represents, the math on the two time variables is done correctly down to the second. Perhaps the real question is what is it casting those two time variables into to be able to do the math properly when it can’t do it for an actual time variable?

[WCmore]

Honestly, I think it comes down to Time variables do not like to store seconds, LOL
(meaning a ‘dumb’ string retains the most accurate answer)

In other words, I suspect the math is done properly in all of your examples, but the storage canister for Time is restrictive.

To test this, you can convert that perfect string into Time, and watch the seconds disappear…

[guxdude]

I believe the time variable doesn’t have a problem with storing seconds. In fact I believe I have narrowed the issue down to the cast function from string to time (or datetime). I created the test piston below and it shows whenever you cast from string to time, seconds are lost. Casts from time to integer (see seconds and milliseconds calculation) or integer to time (see ‘…S’ variables) retain the seconds. Note when there is not cast (’…NF’ variables) the seconds are also retained. Also, in answer to your question above, the dynamic version is using string because that is the output of formatDuration. In the case of dynamic data, no cast is performed.