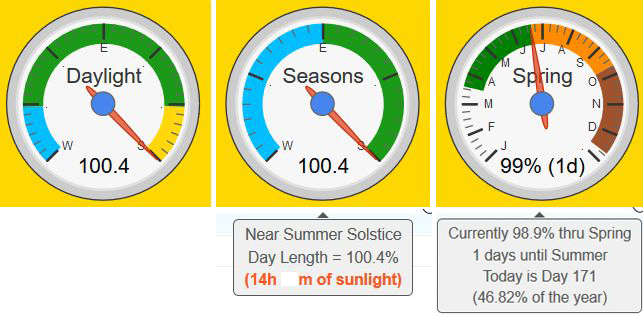
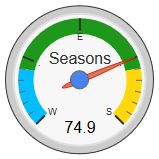
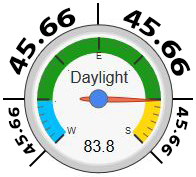
I made a piston a few months ago, and I think it is time I shared it with others. This one draws a gauge on my dashboard that monitors the amount of sunlight on any particular day. Basically, far left on the dial is the Winter Solstice (the shortest day of the year) and the far right is the Summer Solstice (the longest day of the year). When the dial is straight up (50) it is one of the 2 Equinoxes (days and nights are equal).
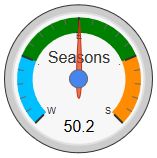
(This picture was saved a few hours after our last Equinox)
There is a bit of math required to get this one customized to your location, but if you are interested, keep on reading. (The first few steps are done with a calculator, pen and paper)
First, you need to find the longest and shortest days for your location (down to the seconds for accuracy). I put in my city at www.timeanddate.com/sun/ and then examined the “Daylength” in late June and then in late December to find the extremes. Take note of the longest time in June, and the shortest time in December.
(For me, it was 14h 01m 57s and 10h 22m 24s) <<-- This last time will be used in webCoRE
Next, we need to convert those times to something understood by webCoRE.
Use the Evaluation Console as an expression something like this:
datetime('14:01:57')
-and-
datetime('10:22:24')
Use your numbers instead of mine, and make note of both responses.
(for me, it was 1529607660000 & 1529594520000)
Next, subtract the small number from the larger number.
(For me, it was: 1529607660000 - 1529594520000 = 13140000) <<-- This number is used in the next step
This answer tells me that in my city, there is 13,140 seconds (3.65 hours) difference between the amount of daylight between the two Solstices.
Next, we want a conversion rate of 100, where 0 would be the shortest day, and 100 would be the longest day. So (getting as many decimal places as we can) we do this formula:
100 / 13140000 = 0.000007610350076103501 <<-- This last number will be used in webCoRE
(make sure you replace my 13140000 with your number)
Then in webCoRE, we make a piston:
define
integer dayLengthLong
decimal dayLengthPercent
end define
Every day, at 15 seconds after midnight
do
Set variable {dayLengthLong} = {datetime(formatDuration($sunset-$sunrise, false, 's'))}
Set variable {dayLengthPercent} = {(dayLengthLong - datetime('10:22:24')) * 0.000007610350076103501}
Set variable {@@dayLengthPercent} = {round(dayLengthPercent,1)}
Notice this last variable is a GLOBAL variable so it can be referred to by other pistons. Also make sure you substitute your December shortest time where I have 10:22:24 above, and your ultra small number in place of my 0.000007610350076103501
Alright, the preparation math is done. Now we are moving on to drawing the gauge.
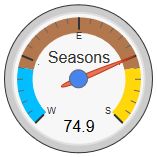
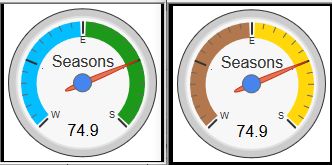
Set piston tile #1 title to "[chart-gauge min=0 max=100 greenFrom=0 greenTo=25 greenColor=DeepSkyBlue yellowFrom=25 yellowTo=75 yellowColor=Green redFrom=75 redTo=100 redColor=DarkOrange minorTicks=6 majorTicks=W.E.S|Seasons]" text to "{@@dayLengthPercent}", footer to "{{@@dayLengthPercent}}", and colors to whatever.
Set piston state to "{"Day Length = "@@dayLengthPercent"% @ "$time}";
And there you have it! A great ‘bird’s eye view’ of where we are in the yearly cycle.
Edit:
For those who are a bit overwhelmed by this manual approach, I have a piston below that can be imported. (although you will miss some good posts if you jump right to post #52)







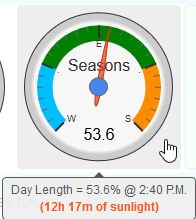
 & 16%
& 16% daylight changes around the December Solstice (16-0-16%)
daylight changes around the December Solstice (16-0-16%)