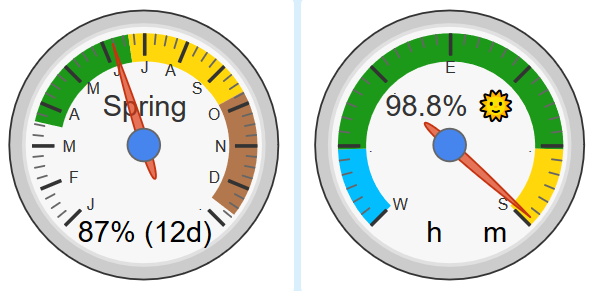
Ten days until the Equinox.
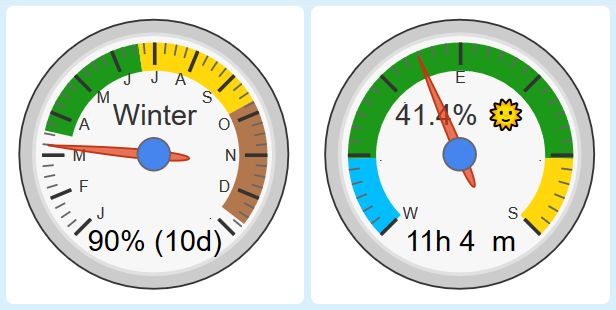
Notice how significant the right gauge moved in the past 11 days!!
(that much change could take 5-6 weeks near the Solstices)

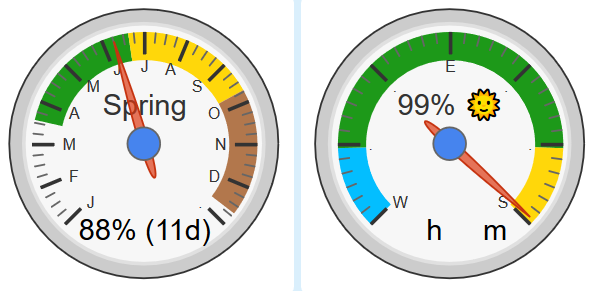
Ten days until the Equinox.

Notice how significant the right gauge moved in the past 11 days!!
(that much change could take 5-6 weeks near the Solstices)
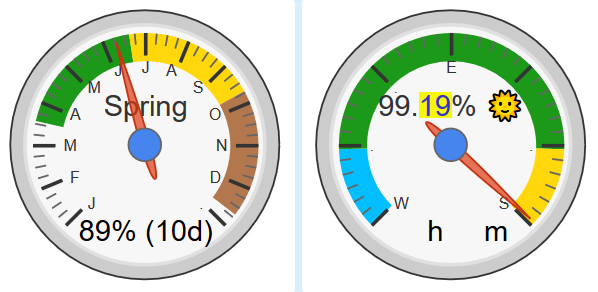
The Equinox has come and passed, but I stalled a few days to be able to showcase this…
Here is 9 days straight… (4 days before and 4 days after the Equinox)
I still find it interesting how the “equal day & night” takes place a few days before the Equinox… not during, as we are taught growing up… (how many days depends on your latitude)
Also worth noting is how the dayLengthPercent crossed 50% about 1.1 days after the Equinox…
I should probably mention that even though the right gauge only displays hours & minutes, the math behind the scenes are actually measuring precise seconds, so this is what is actually happening in real life.
(IE: the day after the Equinox, the dayLength was dead center between the two Solstices)
[ pic from today ]
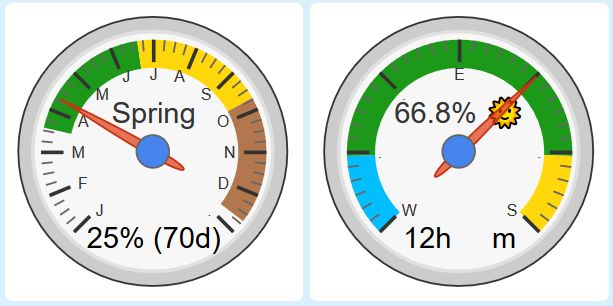
This signifies that we have left the 6 weeks period with the largest increases in daylight day-to-day.
We are exactly half-way through Spring now…
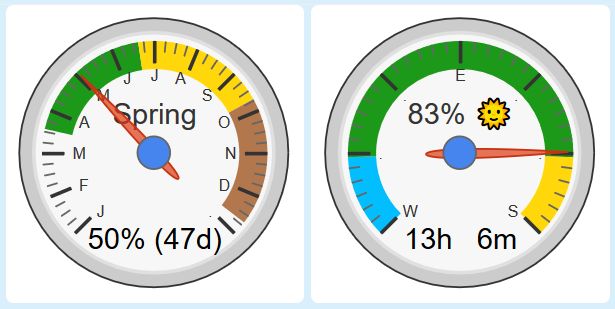
For those of us north of the equator, today begins the 3 month quarter with the most amount of sunlight.
.
I’m still trying to think of a good name for this time period. (roughly May thru July)
This one’s not as easy as “Darkember”
I finally got around to creating this…now I need to find some time to create the gauges…
Now my wife will say I have over 14 hours of daylight to do work around the house. 
Sorry about this unintended side-effect, LOL
If it helps, here is my latest snippet for my gauge: (using the ‘Value’ field)
[chart-gauge min=0 max=100 greenFrom=0 greenTo=16 greenColor={colorWin} yellowFrom=16 yellowTo=84 yellowColor={colorYel} redFrom=84 redTo=100 redColor={colorSum} minorTicks=6 majorTicks=W…E…S|{dlpR}%  ]
]
{colorWin} and {colorSum} are static, while
{colorYel} changes based on what day of the year it is… Something like:
(isBetween(doy,172,356) ? 'colorFall' : 'colorSpring')
{dlpR} is actually {dlp} rounded…
isBetween(dlp,1,99) ? round(dlp,1) : round(dlp,2)
It shows a single decimal most of the year, but two decimals from 0-1% and 99-100%.
Let me know @Koyfam if you need any help setting this up…
It is definitely one of my favorite pistons…
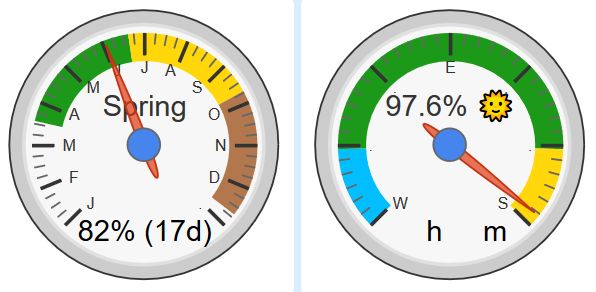
(the references above are for the right gauge… with time removed for privacy)
I may definitely take you up on this offer. I’ll plaY around with it first and reach out if I get stuck or have questions.
I admit, I feel bad I have not uploaded a piston’s import code to draw those gauges… My complexity in that piston has reached a high level of personalization at this point, so I am unable to share it.
(For example: It pulls extra data from a private API, and references @globals that you do not have)
To share it here, I would have to copy it, and strip out 90% of the code first.
(would you guys even want this?)
I mean technically, it is only a single line of code to draw a gauge… Mine only got complicated because I wanted a different color for Spring / Fall. If you don’t care about that, it is literally just a single line of code referencing that @dayLengthPercent global.
In my defense, when I normally share pistons publicly, I try to do it after extensive testing, but before personalizing them to my household. (IE: You guys in the forums never see my final draft)
In this particular case, my gauge piston advanced too far before I was happy with it…
… and when I was happy with it, it was already too personal to share.
I just wanted to showcase this code snippet in action…
This tweak uses 1 decimal most of the year, but switches to 2 decimals during the slow time period.
(typically the 10 days on either side of the Solstices)
Monday:
Tuesday:
(note the real @dlp was 98.996% here)
Wednesday:
(the double decimals should linger for about 20 days, then switch back to a single digit)
Essentially, this gives me precision when I need it most, and a great birds-eye-view for the rest of the year.
Not sure if my math may be off but I’m already at 100% daylight. I got a basic gauge to work. Need to fine tune it.
If you are using $sunset and $sunrise for times, it always rounds down.
(IE: 6:30:59 is displayed as 6:30)
This removes a tad bit of accuracy…
For what it’s worth, sticking with the simple $sunset and $sunrise times should keep you within about 0.5% of total accuracy. (it depends on your latitude… My worst case last year was off 0.42%)
I am currently using:
$twcweather.conditions.sunriseTimeLocal
$twcweather.conditions.sunsetTimeLocal
which brings in actual seconds.
(although it requires a bit more math to calculate)
I still had your prior calculation piston using $sunrise/$sunset. I assume the extra calculations is just converting the ISO time to a regular datetime? Since it is Local, does that mean I don’t need the tzOffset? thanks.
FYI: When I put these calculations in my dlp when from 99.33% to 99.66%. More than just what I would expect from 3am to now.
In this case, I don’t use dateTime… I use a time variable. (set by another piston)
IE:
time @sunrise 6:47:19 AM
time @sunset 7:12:47 PM
but the key element to this whole piston is converting (sunset - sunrise) into seconds.
(we need to know how many seconds the sun is above the horizon… Snippet below)
That is correct. All of the math is within a single day.
(which is automatically compared to your yearly expectations)
Here is a tiny snippet referring to my @global:
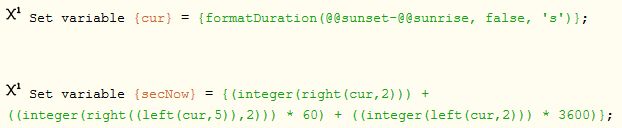
{cur} is a string, and {secNow} is an integer…
For example, 7:03:06pm - 6am = 13:03:06
then we want (6) + (3 * 60) + (13 * 3600) = 46,986 seconds of sunlight
That is an acceptable level of margin using floor rounded minutes.
Mine is now within 0.04% accuracy using the seconds of sunrise and sunset.
Remember, this @dlp percent only changes once a day…
You can run it at 1am, noon and 11pm, and the daily numbers will all be the same.
OK, got it now. Funny I forgot abut the machinations required to get seconds into the time variable. When I first put in the TWC sunrise and sunset it was still truncating the seconds. I updated to this:
Which gives me the full time and now I am back to 99.32%. So the old calculation was only off by 0.01%.
I see what you are doing here… You are letting webCoRE floor the minute, then just add the final seconds afterwards.
Slick.
(although it does triple the calls to $twcweather)
I thought these were just variables. I know they update periodically but assumed they were just static otherwise. Does each reference to $twcweather make some sort of call? I had a different implementation that stuck the values into intermediate variables and processed on that but I didn’t think it made a difference. That would do the same thing with just one ‘call’ for each value. I guess my other question is how do you convert to your sunrise/sunset variables from $twc given the time() conversion truncation?
From what I can see, every $twcweather command pulls fresh data…
(even if the data has not updated in awhile)
Two steps really. One piston runs daily and sticks the time into a global string:
… and then this piston takes that @global string, and does my previously mentioned math.
I mean, you could do both in the same piston… I just have mine set up to update at different times, with different parameters.
Pro Tip:
You probably want your @globals to only use a single @…
(not two like in my examples)
Sorry, I’m slow today. I think you showed here how you store the string {@@sunsetStr} and you showed above how you do calculations based on a time variable {@@sunset} but my problem was converting from a string to time as @@sunset=time(@@sunsetStr) would truncate the seconds. Was wondering if you had some trick other than what I did above to ensure you got the seconds.
I don’t think I converted the string into Time… I just went thru the work to go the other way…
(converting the time into a string, LOL)
Highlights from my earlier posts:
I set the global:
time @sunrise 6:47:19 AM
time @sunset 7:12:47 PM
Then I subtract those @global times and store in a string {cur}. (first line below)

Then I parsed the string… (second) + (minute * 60) + (hour * 3600) (last line above)
This tells us the exact number of seconds that the sun is above the horizon…
To answer this another way, here are the three steps I went with: (Time > String > Integer)
@sunrise = 6:47:19 AM and @sunset = 7:12:47 PM
{cur} = 13:18:29
{secNow} = 47909 <-- This is the number that is inputted into all of the other math(it could really be done in 1 or 2 steps, but I want the @global for other pistons to use, and {cur} is a great abbreviation for my piston state)
Notice I manually do the math in the last step to assure that the seconds are counted.
![]()
Using my {cur} example above, this is: (29) + (18 * 60) + (13 * 3600)
(If you let webCoRE calculate normally, you will loose the precious seconds, due to flooring… which probably explains your 0.01% variance)